Mendelian randomization (MR)

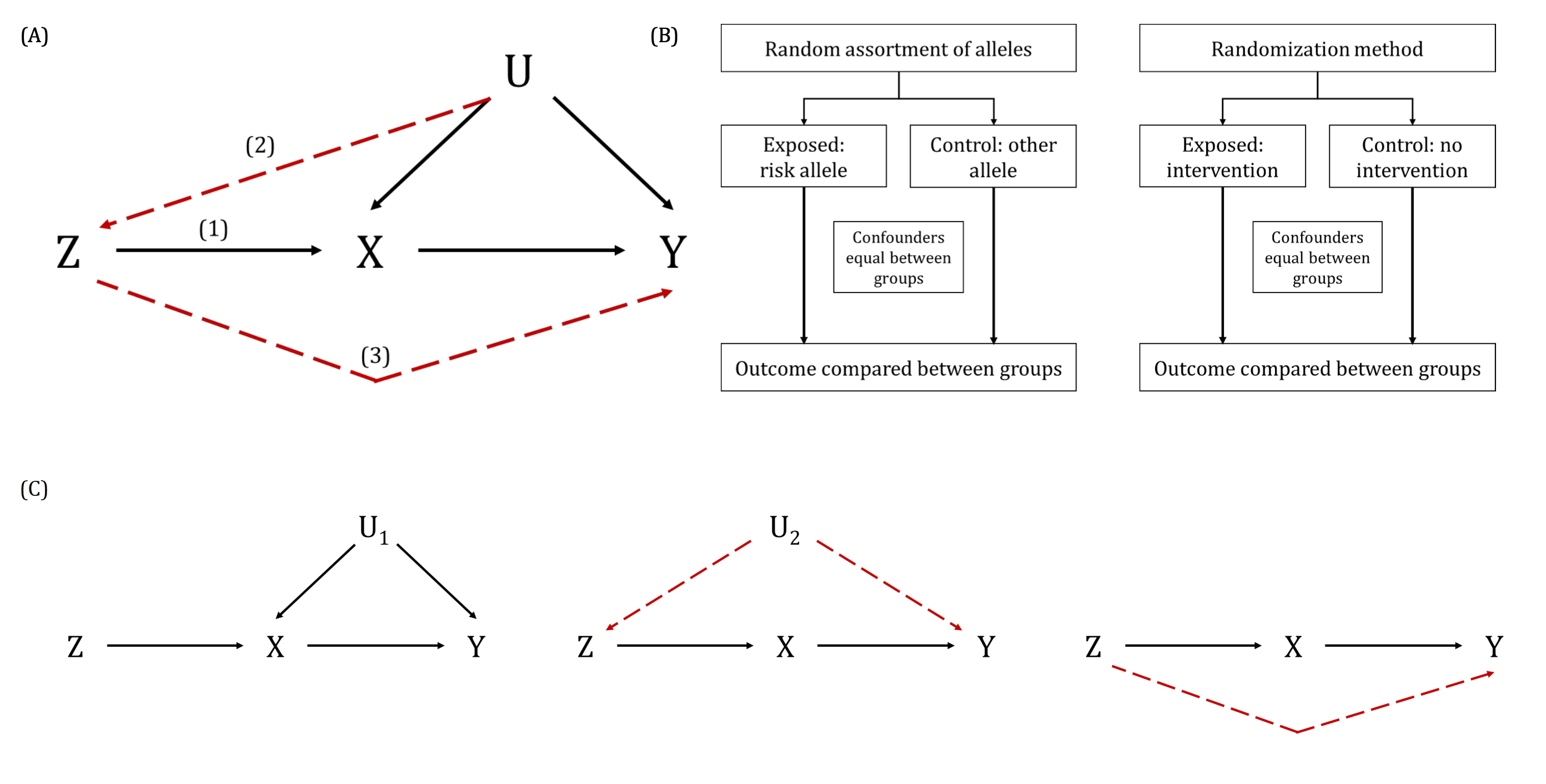
Synonyms: Mendelian randomisation (MR)

A method that uses genetic variants as IVs to explore causal effects of risk factors on outcomes in observational epidemiological studies.

Genetic IVs must fulfil the same assumptions as IVs. In most MR studies, the assumption that is most likely to be violated is the exclusion restriction assumption due to horizontal pleiotropy.

References

• Lawlor DA, Harbord RM, Sterne JAC, Timpson NJ, Davey Smith G. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Statistic in Medicine 2008;27:1133-1163.
• Davey Smith G, Ebrahim S. "Mendelian randomisation": can genetic epidemiology contribute to understanding environmental determinants of disease? International Journal of Epidemiology 2003;32:1-22.

Other terms in 'Definition of MR and study designs':

• Bidirectional MR
• Binary exposure MR
• Factorial MR
• Instrumental variable (IV)
• Multivariable MR
• One-sample MR
• Two-sample MR
• Two-sample MR with individual participant data (IPD)
• Two-sample MR with summary (aggregate) data
• Two-step/Mediation MR