MR Dictionary

Two-sample MR or MR with summary-level data

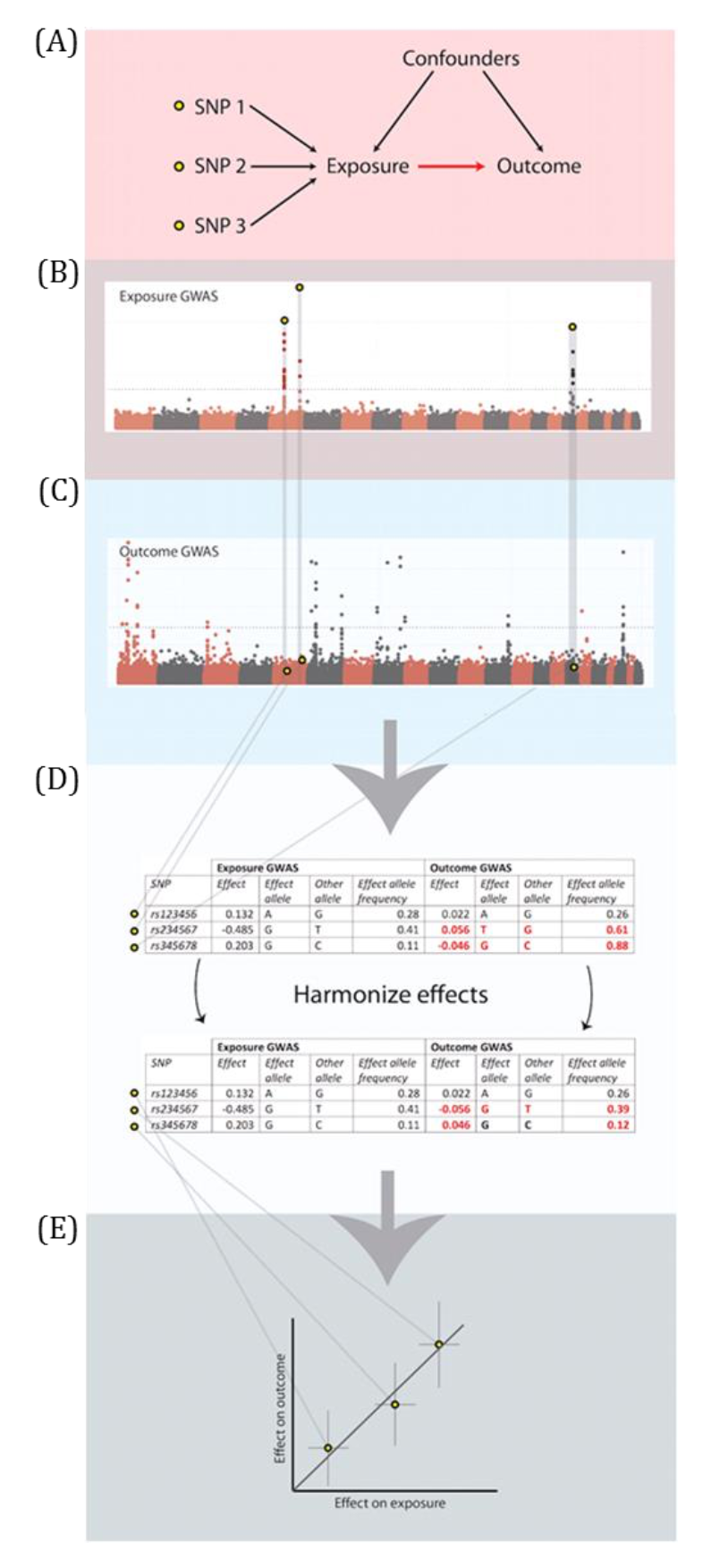
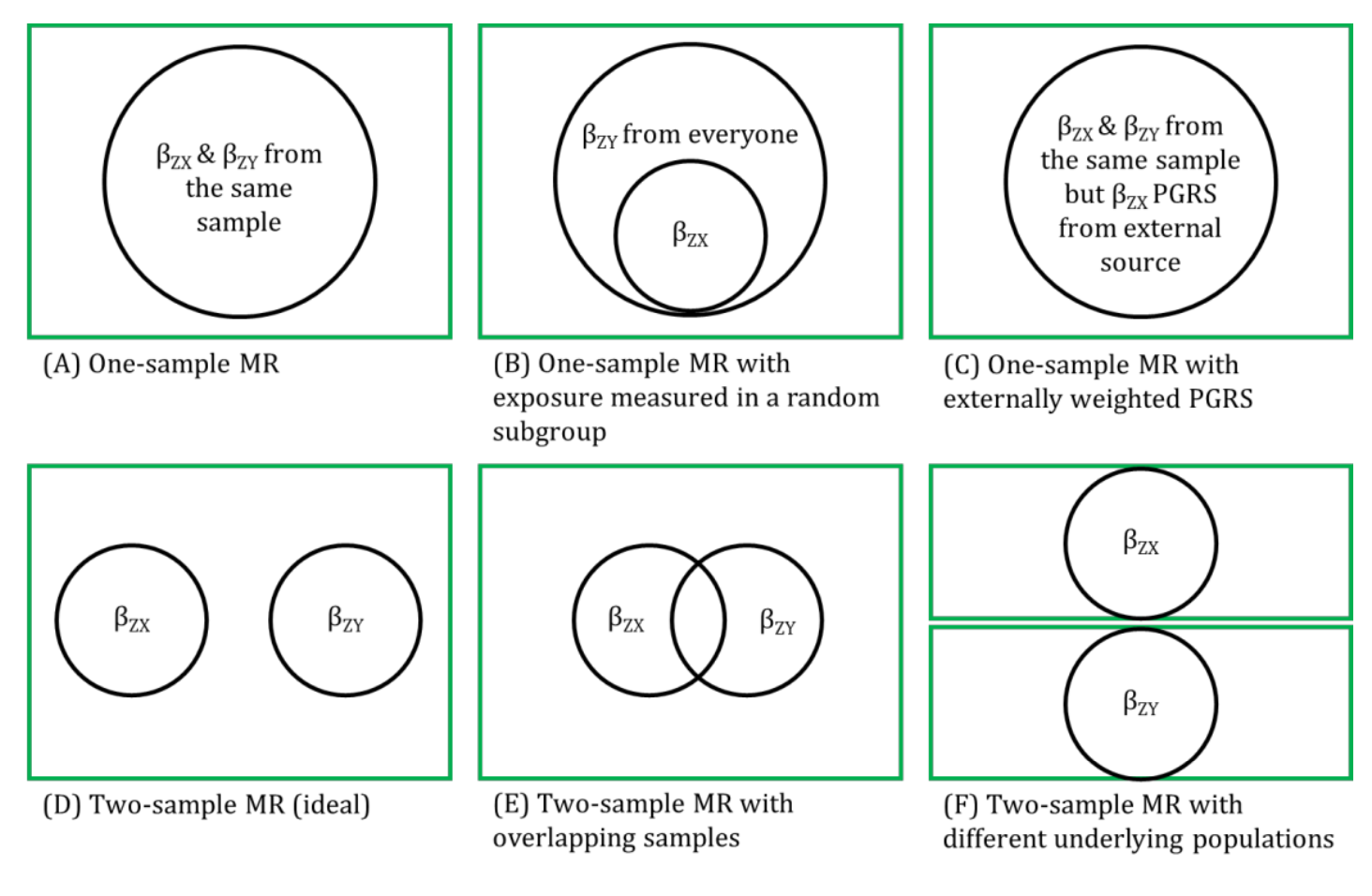
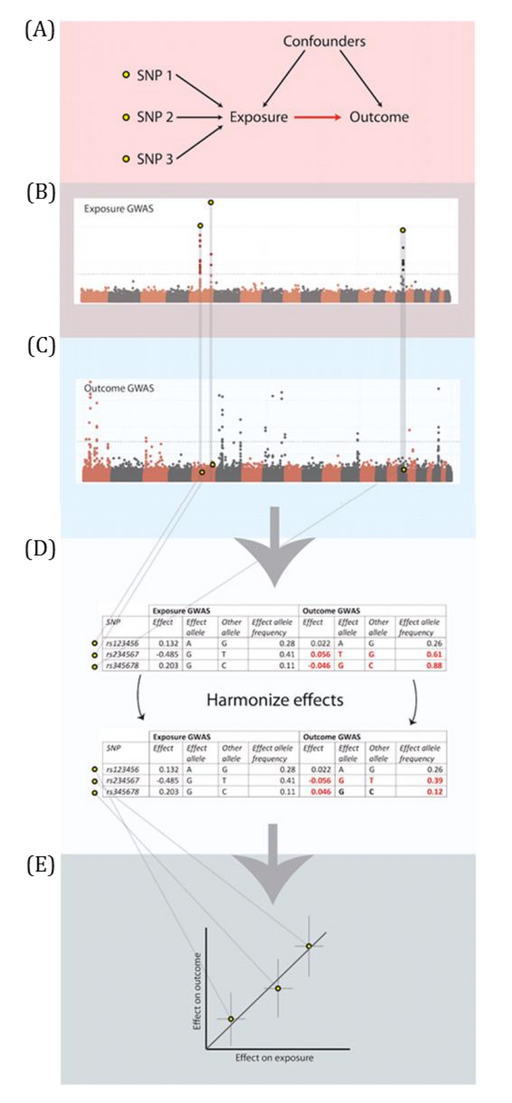
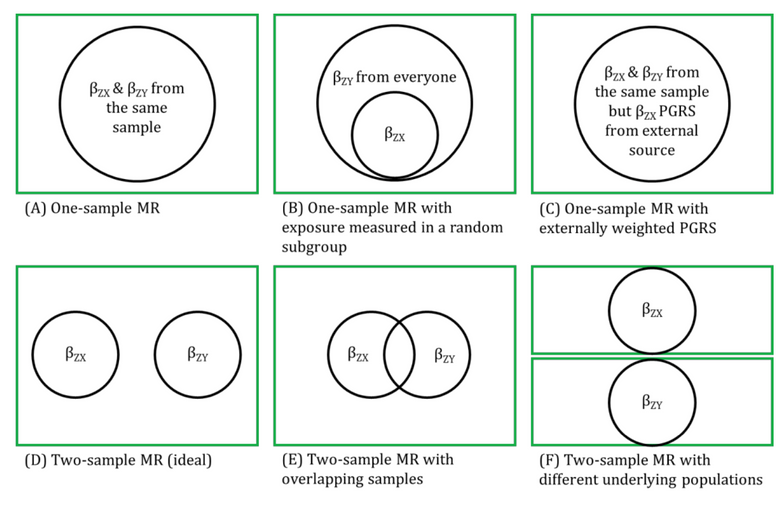
MR analyses in which the associations between the genetic instrumental variable (IV) and exposure and the genetic IV and outcome are generated from different (non-overlapping) samples and summary-level data are used to derive the MR estimate.

Genetic IVs must fulfil the same MR assumptions. Genetic IVs associated with the exposure of interest are usually identified and summary-level data (e.g., betas, standard errors and p-values) describing the IV-exposure association are obtained from a genome-wide association study (GWAS) of the exposure. Summary-level data of those same exposure-related IVs are usually then extracted from a GWAS of the outcome. These summary-level data describing the IV-exposure and IV-outcome associations are then used to estimate the causal effect between the exposure and outcome. Equally, individual-level data can be used to derive these summary statistics if individual-level or individual participant data (IPD) is available. In this setting, there is more potential (than with summary-level data) for assessing the associations between the genetic IV with observed confounders of the exposure-outcome association and exploring interactions, non-linear or subgroup effects. With summary-level data, it may be difficult to ensure the two samples are from the same underlying population and non-overlapping. Two-sample MR is less prone to data overfitting than one-sample MR. In two-sample MR, weak instrument bias will tend to bias the estimate towards the null. Conversely, weak instrument bias in a one-sample MR will tend to bias the estimate towards the confounded multivariable regression estimate. Though, if there is overlap of participants in the two samples used for two-sample MR, the direction of any weak instrument bias in a two-sample setting will tend towards the confounded multivariable regression estimate (i.e., like in a one-sample setting with individual-level data) approximately proportional to the amount of overlap. Correct harmonization of alleles across the two samples is essential. The two samples should be from the same underlying population but should be (largely) non-overlapping. The IV-exposure and IV-outcome models must be correctly specified. NOTE: there are grey areas between one-sample and two-sample MR (e.g., in two-sample MR, where two samples have some overlap, as shown in Figure 2.6, or when one sample of individual-level data has been used to generate summary statistics that contribute to the derivation of the MR estimate using methods derived for a two-sample MR setting). In fact, some MR studies use a mixture of analyses conducted in both individual- and summary-level data, sometimes using the same population sample. Therefore, the way in which these methods are described has evolved in the literature to focus on the data source being used in MR analyses rather than the number of samples - i.e., "two-sample MR" is equivalent to "summary-level data MR" or "MR with summary-level data".

Two-sample Mendelian randomization. Adapted from Hemani et al. (A) In two-sample MR, the associations of the instrument(s) with the exposure and outcome are derived from two independent (i.e., non-overlapping) samples. In this example, there are three SNPs acting as genetic IVs for the hypothetical exposure (i.e., SNP1, SNP2 and SNP3). (B) Manhattan plots showing the SNP-exposure estimates for each of the three SNPs are derived from a genome-wide association studies (GWAS) of the exposure variable. (C) The estimates of association between these three same SNPs and the outcome variable are then obtained from the outcome GWAS (results that are also depicted in a Manhattan plot). (D) Effects are harmonized to ensure that the ‘effect’ estimates in both the exposure and outcome GWASs correspond to the same allele (i.e., one that consistently either increases or decreases the exposure variable) for each SNP. (E) Once effects are harmonized, MR analyses can be performed. Visually, a scatter plot can be generated to represent the results, whereby the slope of the line is equivalent to the causal estimate. For example, the when using the inverse-variance weighted method, the intercept is held at zero.
Figure 2.5 - Two-sample Mendelian randomization. Adapted from Hemani et al. (A) In two-sample MR, the associations of the instrument(s) with the exposure and outcome are derived from two independent (i.e., non-overlapping) samples. In this example, there are three SNPs acting as genetic IVs for the hypothetical exposure (i.e., SNP1, SNP2 and SNP3). (B) Manhattan plots showing the SNP-exposure estimates for each of the three SNPs are derived from a genome-wide association studies (GWAS) of the exposure variable. (C) The estimates of association between these three same SNPs and the outcome variable are then obtained from the outcome GWAS (results that are also depicted in a Manhattan plot). (D) Effects are harmonized to ensure that the ‘effect’ estimates in both the exposure and outcome GWASs correspond to the same allele (i.e., one that consistently either increases or decreases the exposure variable) for each SNP. (E) Once effects are harmonized, MR analyses can be performed. Visually, a scatter plot can be generated to represent the results, whereby the slope of the line is equivalent to the causal estimate. For example, the when using the inverse-variance weighted method, the intercept is held at zero.
Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.
Figure 2.6 - Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.

References

Other terms in 'Definition of MR and study designs':