MR Dictionary

Same underlying population (in two-sample MR)

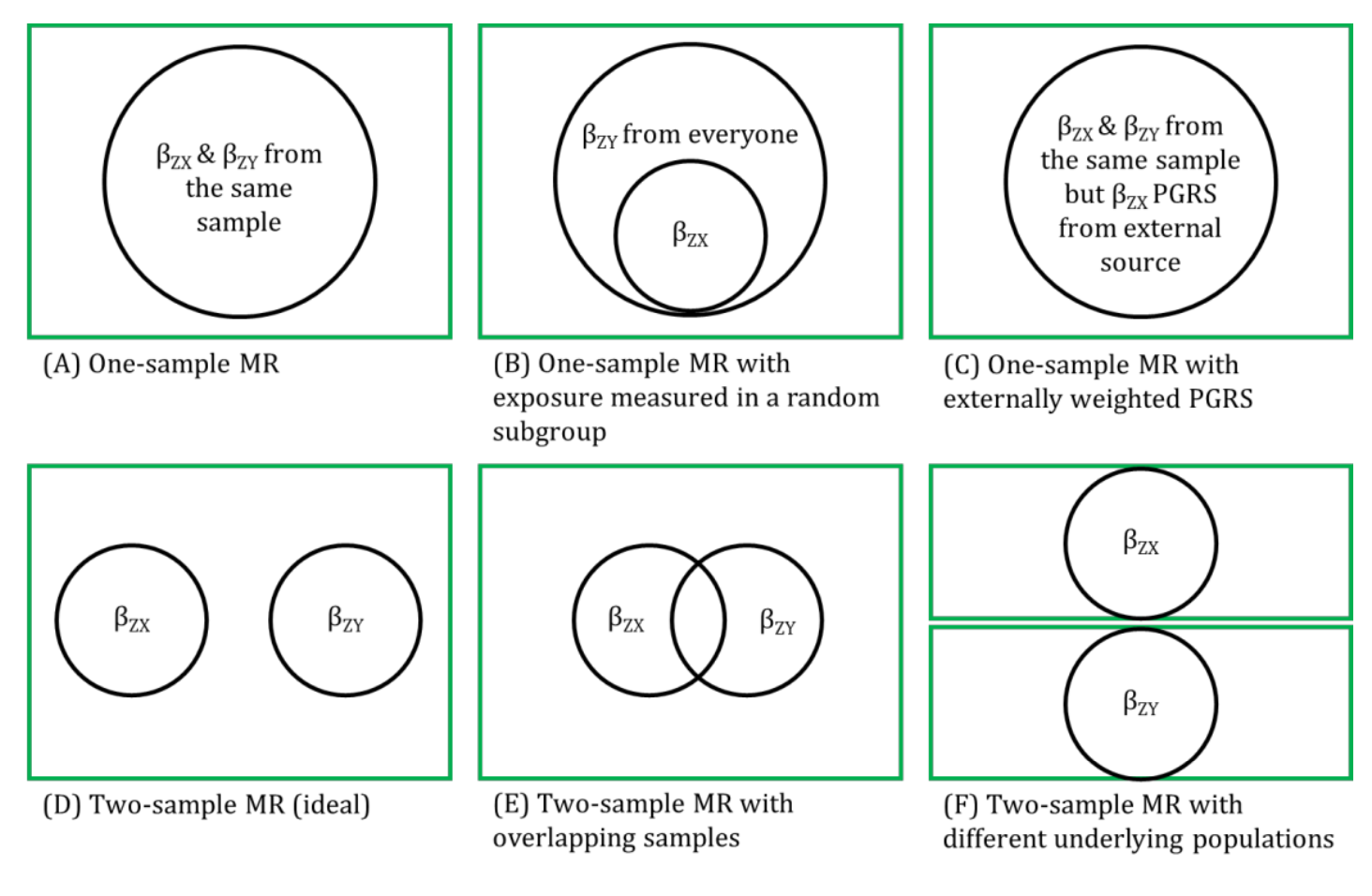
It is important that the associations between both the genetic instrumental variable (IV) and exposure and the genetic IV and outcome in two-sample MR are from the same underlying population. Alternatively, at a minimum, there is evidence that the association between the IV and exposure is similar in the population used for the second sample (i.e., the source of association of the genetic IV and outcome). 

Many genome-wide association studies (GWASs) that are used to identify genetic IVs associated with the exposure for an MR analysis are conducted in women and men combined. If these findings are then combined with data used to source information about the association between those same genetic IVs and the outcome in women only (for example, if the outcome of interest was breast or ovarian cancer), the assumption is that the association between the genetic IV and exposure does not differ between women and men. Ideally, the two samples would be from the same underlying population. If this is not possible (e.g., because aggregate data being used and the populations differ in the two samples), some attempt should be made to find evidence that the associations between the genetic IV and exposure is similar in the population used to source the association between the genetic IV and outcome, as in the original GWAS. 

Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.
Figure 2.6 - Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.

References

Other terms in 'Sources of bias and limitations in MR':