MR Dictionary

Overfitting

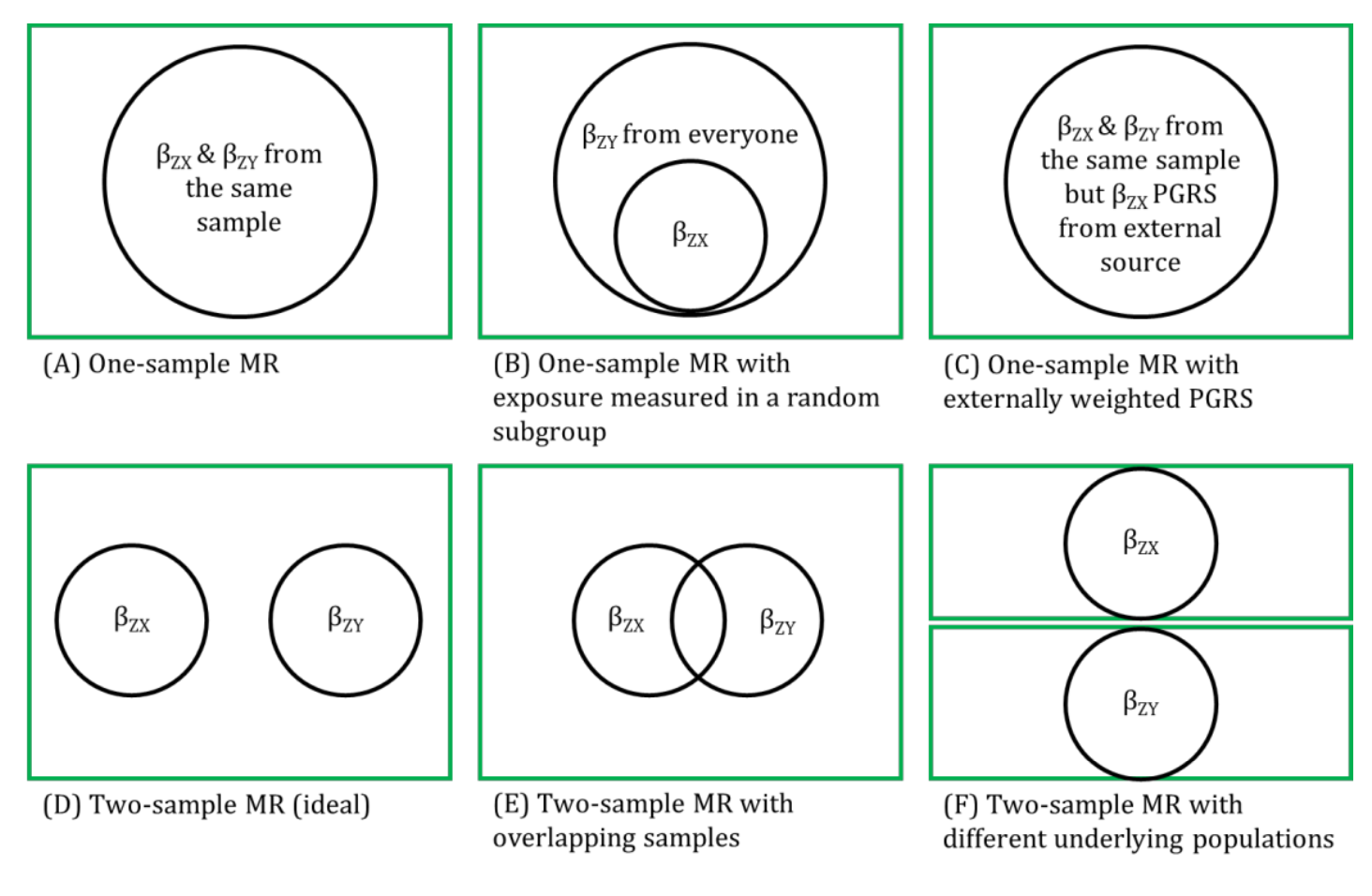
This refers to exaggerated results, whereby there is a bias of estimates away from the null, occurring when MR studies are done within the same sample (e.g., the sample that contributed towards the genome-wide association study (GWAS)) from which the genetic instrumental variables (IVs) are selected. 

Ideally, selecting genetic IVs from the same study in which the MR analysis is being conducted should be avoided to reduce this overfitting. Using weighted polygenic risk score (PRS) in one-sample MR where the weights of the genetic IV-exposure association are taken from an independent GWAS minimises bias due to overfitting. Two-sample MR, where genetic IV-outcome associations are obtained from an independent GWAS from the GWAS of the exposure, and there is little or no overlap between the two samples, avoids overfitting. 

Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.
Figure 2.6 - Relationship of one-sample and two-sample Mendelian randomization: populations and samples. In all examples, the green box represents the same underlying population from which samples are drawn; the black circles represent the samples and the text in these summarises the source of association of genetic instrument with exposure (βZX) and association of genetic instrument with outcome (βZY). In one-sample MR (A) where βZX and βZY are estimated within the same population, there may be over-fitting of the data because the predicted (by genetic IV) values of X are then used to predict Y in the same sample. In this study type, weak instrument bias will be expected to bias towards the confounded result. In one-sample MR, it is not necessary to have exposures measured on all sample participants. For expensive exposures, these could be measured in a subsample (B). The properties and sources of bias will be broadly similar to those in (A), where exposures are measured in all participants, but the likelihood of weak instrument bias may be greater. When βZX is obtained in a one-sample MR study but with external weights (i.e., the association magnitudes taken from a GWAS to which the sample being used for the MR did not contribute), as shown in (C), over-fitting of the data is minimised. Ideally, in two-sample MR, both samples are drawn from the same underlying population but there is no overlap of participants between the two samples, as shown in (D). In this situation, data will not be over-fitted and any weak instrument bias would be expected to bias towards the null. As GWAS get larger, and with more cohorts contributing to them, the potential for overlap between samples in summary data two-sample MR becomes increasingly likely, as shown in (E). The more overlap there is between the two samples, the more effects of over-fitting and weak instrument bias become similar to those seen in one-sample MR. In figure (F), the two samples are drawn from two different underlying populations. This might occur when using MR for testing developmental origins, when βZX is estimated in pregnant women and βZY is estimated in their offspring. In that situation, it is important to consider (and ideally test) whether the βZX association in pregnancy is the same as in non-pregnant females and males (i.e., as in the offspring sample). Similarly, when using aggregate data in two-sample MR and when the outcome of interest can only occur in one sex (e.g., cervical or prostate cancer), ideally one would want aggregate βZX estimates to be sex-specific. If that is not possible, then drawing on other external evidence to consider the extent to which βZX is likely to be similar in females and males is important.

References

Other terms in 'Sources of bias and limitations in MR':